30. 串联所有单词的子串

给定一个字符串 s 和一个字符串数组 words。 words 中所有字符串 长度相同。

s 中的 串联子串 是指一个包含 words 中所有字符串以任意顺序排列连接起来的子串。

  • 例如，如果 words = ["ab","cd","ef"]， 那么 "abcdef"， "abefcd"，"cdabef"， "cdefab"，"efabcd"， 和 "efcdab" 都是串联子串。 "acdbef" 不是串联子串，因为他不是任何 words 排列的连接。

返回所有串联子串在 s 中的开始索引。你可以以 任意顺序 返回答案。

示例 1：

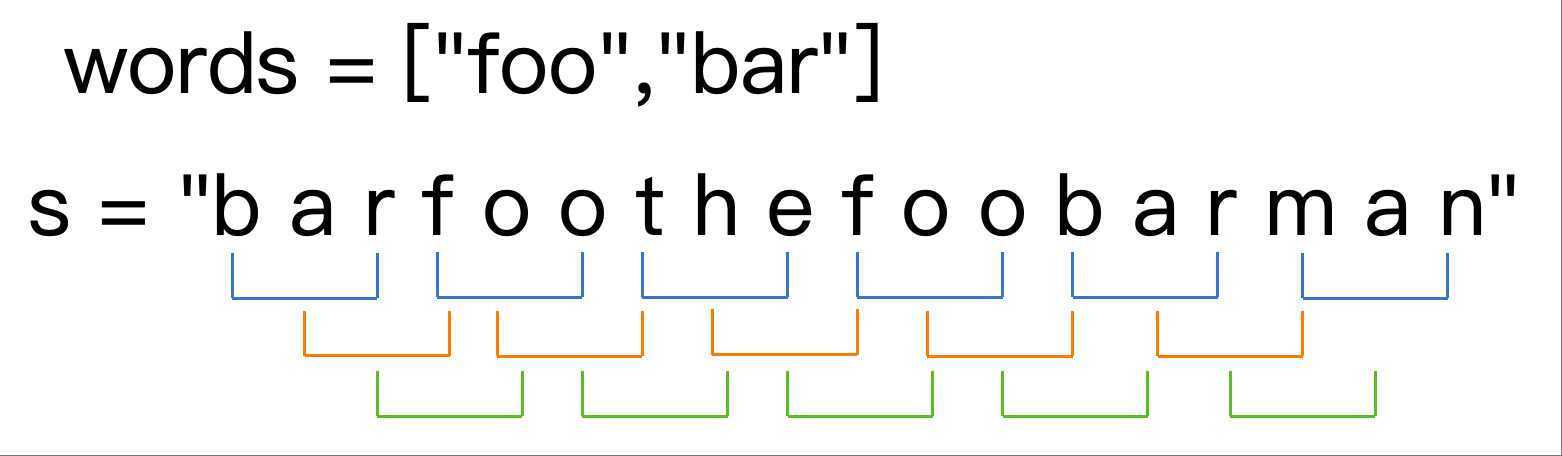
输入：s = “barfoothefoobarman”, words = [“foo”,“bar”]
输出：[0,9]
解释：因为 words.length == 2 同时 words[i].length == 3，连接的子字符串的长度必须为 6。
子串 “barfoo” 开始位置是 0。它是 words 中以 [“bar”,“foo”] 顺序排列的连接。
子串 “foobar” 开始位置是 9。它是 words 中以 [“foo”,“bar”] 顺序排列的连接。
输出顺序无关紧要。返回 [9,0] 也是可以的。

示例 2：

输入：s = “wordgoodgoodgoodbestword”, words = [“word”,“good”,“best”,“word”]
输出：[]
解释：因为 words.length == 4 并且 words[i].length == 4，所以串联子串的长度必须为 16。
s 中没有子串长度为 16 并且等于 words 的任何顺序排列的连接。
所以我们返回一个空数组。

示例 3：

输入：s = “barfoofoobarthefoobarman”, words = [“bar”,“foo”,“the”]
输出：[6,9,12]
解释：因为 words.length == 3 并且 words[i].length == 3，所以串联子串的长度必须为 9。
子串 “foobarthe” 开始位置是 6。它是 words 中以 [“foo”,“bar”,“the”] 顺序排列的连接。
子串 “barthefoo” 开始位置是 9。它是 words 中以 [“bar”,“the”,“foo”] 顺序排列的连接。
子串 “thefoobar” 开始位置是 12。它是 words 中以 [“the”,“foo”,“bar”] 顺序排列的连接。

提示：

  • 1 <= s.length <= 104
  • 1 <= words.length <= 5000
  • 1 <= words[i].length <= 30
  • words[i] 和 s 由小写英文字母组成

题解

比较容易可以想到ss中符合要求的子串长度一定是sublength=words.length×words[i].lengthsublength=words.length\times words[i].length，那么暴力的方法是：

我们假设：

  • NN = 字符串 s 的长度。
  • MM = words 数组中单词的个数。
  • WW = 每个单词的长度 (gap)。
for(int i = 0; i < n; i ++){ //循环遍历s字符串
		string tmp = s.substr(i, sublength); //每次取长度sublength的子串
		if(judge(tmp)) ans.push_back(i); //判断是否符合要求
}

外层循环：执行 NN 次；字符串截取：s.substr(i, sublength)；长度为 M×WM \times W。耗时 O(M⋅W)O(M \cdot W)，Judge 函数（假设实现）： 为了判断 tmp 是否由 words 组成，通常需要：将 tmp 切割成 MM 个长度为 WW 的单词，构建一个新的哈希表统计频率，与原 words 的哈希表比对，构建哈希表代价：MM 个单词，每个插入耗时 O(Wlog⁡M)O(W \log M)。总计 O(M⋅Wlog⁡M)O(M \cdot W \log M)。

总时间复杂度：$$O(N \times (M \cdot W + M \cdot W \log M)) \approx O(N \cdot M \cdot W \cdot \log M)$$ 会超时

题目关键在于如何遍历所有可能的解，考虑改变外层循环为循环gapgap，即每个单词的长度，且每次循环的间隔也为gapgap，即：

for(int i = 0; i < W; i ++){
		.......
}

按照每个单词的长度进行循环，每次间隔WW的长度，即可遍历所有组合，再辅以双指针，初始状态在确定的“起跑线”上，l 和 r 维护一个动态窗口：

  • 进窗口 (r)：r 每次向右跳 gap 长度，截取一个新单词，加入临时哈希表 hash2 计数。
  • 出窗口 (l)：一旦当前窗口长度（r - l + 1）超过了目标总长度（sublength），l 就向右跳 gap 长度，把最左边的那个单词从 hash2 中减去。

当窗口长度正好等于目标总长度（r - l == sublength）时，触发检查逻辑。遍历标准答案 hash 中的每一个单词，去对比它在当前窗口 hash2 中的数量：如果所有单词的计数都完全一致，说明找到通过，记录 l。只要有一个单词数量对不上，就标记失败。

S:  [ a b c ] [ d e f ] [ g h i ] ...
    ^         ^
    l         r
    
    1. r 右移，吃进 "abc"，查表记录。
    2. r 继续右移，吃进 "def"，查表记录。
    3. 如果长度超标，l 右移，吐出 "abc"。
    4. 如果长度达标，对比 hash 和 hash2 是否完全相等。

代码

class Solution {
public:
    map<string, int>hash;

    vector<int> findSubstring(string s, vector<string>& words) {
        int n = s.length(), gap = words[0].size();
        int sublength = gap * words.size(); 
        vector<int> ans;

        for(auto &i: words){
            hash[i] ++;
        }
        for(int i = 0; i < gap; i ++){
            map<string, int> hash2;
            int l = i, r = i;
            string tmp = "";
            while(r <= n - gap && l <= r){
                string t = s.substr(r, gap);
                hash2[t] ++;
                while(r - l + 1 > sublength){
                    string out = s.substr(l, gap);
                    hash2[out] --;
                    l += gap;
                }
                r += gap;
                if(r - l == sublength){
                    bool flag = false;
                    for(auto [ss, cnt]: hash){
                        if(hash[ss] != hash2[ss]){
                            flag = true;
                            break;
                        }
                    }
                    if(!flag){
                        ans.push_back(l);
                    } 
                }
            }
        }
        return ans;
    }
};